Mastering fractions, decimals, and percentages is essential for success on the ASVAB Math Section. These topics frequently appear in Mathematics Knowledge and Arithmetic Reasoning questions. Below is a well-organized study guide with key concepts, formulas, and examples to help you strengthen your math skills.
Fractions
Multiplying Fractions
Rule: Multiply the numerators and multiply the denominators.


Dividing Fractions (Flip It & Multiply)
Dividing fractions is almost as easy as multiplying! You just need to flip and multiply using these steps:
Steps for Dividing Fractions
- Flip the second fraction (take its reciprocal).
- Multiply the first fraction by this flipped fraction.
- Simplify the result if necessary.



Adding & Subtracting Fractions
With a Common Denominator
When fractions have the same denominator, the process is simple!
Steps:
- Add or subtract the numerators (top numbers).
- Keep the denominator the same.
- Simplify if needed.



With Different Denominators
Steps:
- Find the Least Common Denominator (LCD).
- Convert fractions to have the same denominator.
- Perform the operation.

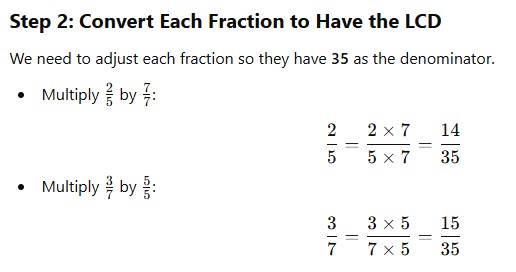


Finding Common Denominators for Three or More Fractions
When adding or subtracting three or more fractions, you follow the same process as for two fractions—find the Least Common Denominator (LCD), convert the fractions, then add or subtract.
Steps:
- Find the Least Common Denominator (LCD)
- The LCD is the smallest multiple that all denominators share.
- Convert each fraction
- Multiply each fraction by the necessary factor to make the denominators the same.
- Add or subtract the numerators
- Keep the denominator the same.
- Simplify if needed

Reducing (Simplifying) Fractions
Steps for Simplifying a Fraction:
- Find the Greatest Common Divisor (GCD) of the numerator and denominator.
- Divide both the numerator and denominator by the GCD.
- Write the simplified fraction.
Mixed Numbers & Improper Fractions
Steps:
- Multiply the whole number by the denominator.
- Add the numerator to the result.
- Write the sum as the new numerator, keeping the same denominator.

Convert Mixed to Improper
Steps:
- Multiply the whole number by the denominator.
- Add the numerator to the result.
- Keep the denominator the same.

Decimals
Multiplying Decimals
Ignore decimals while multiplying, then place the decimal point correctly.
Example:
4.2×3.5
Multiply normally: 42 × 35 = 1470
Count two decimal places: 14.70
Dividing Decimals
Move the decimal in the divisor until it’s a whole number, then move it the same amount in the dividend.
Example:
4.8÷0.4
Move decimal → 48 ÷ 4 = 12
Adding & Subtracting Decimals
Align decimal points before adding or subtracting.
Example:
7.50
+ 3.27
——-
10.77
Percentages
Converting Between Percentages & Decimals
Move decimal two places left for percent → decimal.
Move decimal two places right for decimal → percent.
Examples:
75%=0.75,0.42=42%
Percentage Calculations
Formula:
Percentage×Number
Example:
30% of 80=0.30×80=24
Real-World Example (Discount Calculation):
A $60 item is on 20% discount.
0.20×60=12
New price: $60 – $12 = $48
Ratios & Proportions
Understanding Ratios
Ratios compare two quantities (e.g., 3:2 or 3/2).
Example:
A class has 15 boys and 10 girls.
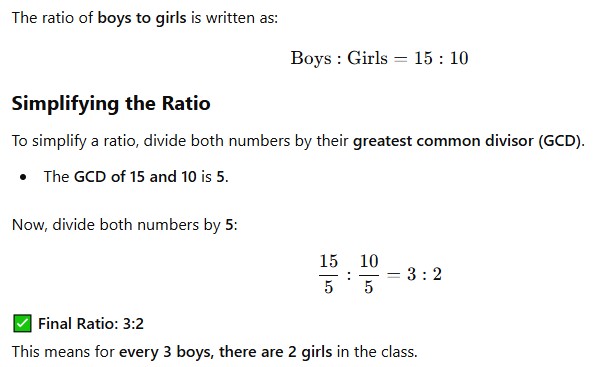
Solving Proportions
📌 Cross-multiply to solve for an unknown in a proportion.
✅ Example:


Rates & Speed Calculations
Speed Formula
Formula:
Speed=Distance/Time
Example:
A car travels 120 miles in 3 hours. Find its speed.
120/3=40 mph
Final Review
- Multiply/Divide Fractions using “Flip & Multiply” for division
- Convert between Mixed & Improper Fractions
- Find Common Denominators before Adding/Subtracting
- Multiply/Divide Decimals by counting decimal places
- Move decimal two places for Percentage-Decimal conversions
- Ratios compare quantities; Proportions solve for unknowns
- Use the Speed Formula: Distance ÷ Time
Next Section: Squares, Roots, Irrational Numbers, Polynomials
Previous Section: General Math and Operational Knowledge

